3.3.6. Ổn định tổng thể của cấu kiện chịu uốn

Xét một dầm chữ I chịu uốn trong mặt phẳng độ cứng lớn nhất:
- Khi mômen uốn nhỏ hơn một trị số nhất định, dầm chỉ võng trong mặt
phẳng thẳng đứng; một nguyên nhân ngẫu hiên gây uốn trong mặt phẳng
ngang hay gây xoắn dầm, nếu nguyên nhân này không còn nữa thì dầm lại trở về trạng thái ban đầu: dầm ổn định uốn.

- Khi M tăng tới một giá trị gọi là tới hạn, trạng thái cân bằng uốn phẳng không là ổn định nữa, mà là chuyển sang trạng thái cân bằng uốn xiên và xoắn. Dầm chuyển sang trạng thái cân bằng mới khác về chất, ta gọi là dầm mất ổn định dạng uốn xoắn. Tải trọng (hay mômen uốn) làm dầm mất ổn định gọi là tải trọng (hay mômen uốn) tới hạn.
Khi cấu kiện chịu uốn, hai thớ trên và dưới sẽ chịu nén và kéo. Tải trọng tới hạn xác định khi vùng nén của dầm xu hướng mất ổn định. Dầm bị uốn ngang và xoắn kiềm chế.
Lý thuyết tính ổn định tổng thể của dầm tương tự thanh chịu nén: trạng thái tới hạn đạt được khi công nội lực khi biến vị cân bằng với thế năng biến đổi hình dạng Ai  Ae .

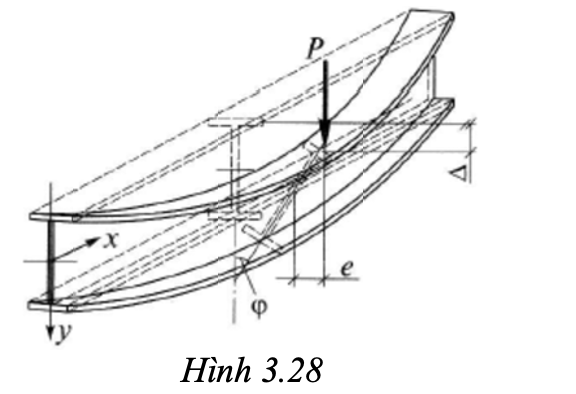
Công nội lực bằng tổng công do uốn ngang Am và xoắn kiềm chế At . Nếu đặt lực tập trung P (hình 3.28), gọi  là góc xoay của tiết diện dầm,  thay đổi theo chiều dài dầm, có  k sin(x / l ), l- chiều dài dầm. Khi đó mômen uốn của dầm trong mặt phẳng ngang

M( x)  ( P/ 2 )xsin  ( P / 2 )x  ( kP/ 2 )xsin(x / l )
Công của nội lực do uốn:

Giá trị c phụ thuộc vào điều kiện liên kết hai đầu dầm, dạng tải trọng (tập trung hay phân bố đều) và vị trí của nó theo chiều cao tiết diện. Trong trường hợp trên c=17,2.
Khi dầm bị xoắn, xuất hiện thêm độ lệch tâm e so với tâm uốn của tiết diện (hình 3.28).
Mômen tới hạn trong dầm Mcr  k1 Pcrl và ứng suất tới hạn cr  Mcr / Wx , ở
đây k1 - hệ số, phụ thuộc vào sơ đồ tính dầm và dạng tải trọng. Khi kiểm tra ổn định tổng thể dầm, ứng suất do uốn được so sánh với ứng suất tới hạn  x  M / Wx  cr c . Đặt b  cr / f

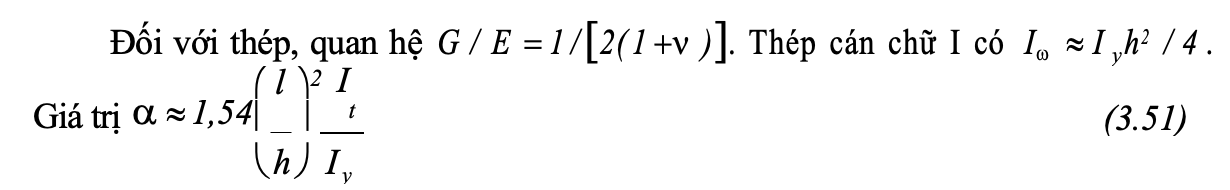
Các công thức trên chỉ đúng khi E= const, hay khi cr tl. Khi đó ứng với b=cr/c tl/c = 0,85. Khi b0,85, dầm mất ổn định ngoài giới hạn đàn hồi.

Trong mọi công thức và tính toán trên phải thay E và G bằng Et và Gt. Việc giải phương trình vi phân trở nên rất khó vì Et và Gt thay đổi theo ứng suất  mà  lại khác nhau dọc chiều dài của dầm. Cách làm gần đúng tìm giới hạn d ới của tải trọng tới hạn là coi Et và Gt không đổi dọc chiều dài dầm và ứng với trị số ứng suất  nén lớn nhất trong dầm, thiên về an toàn.

Trong tính toán theo tiêu chuẩn, dùng hệ số thay đổi tuyến tính b=0,68+0,2l1, 1 tính theo công thức (3.48), nếu 1>1,52 lấy b=1.