3.3.5. Cấu kiện chịu xoắn

Cấu kiện chịu xoắn thường có tiết diện đặc (hình 3.23,a) hoặc tiết diện kín (hình 3.23,b,c). Trên mặt cắt ngang thanh chỉ có ứng suất tiếp do mômen xoắn Mt gây ra:

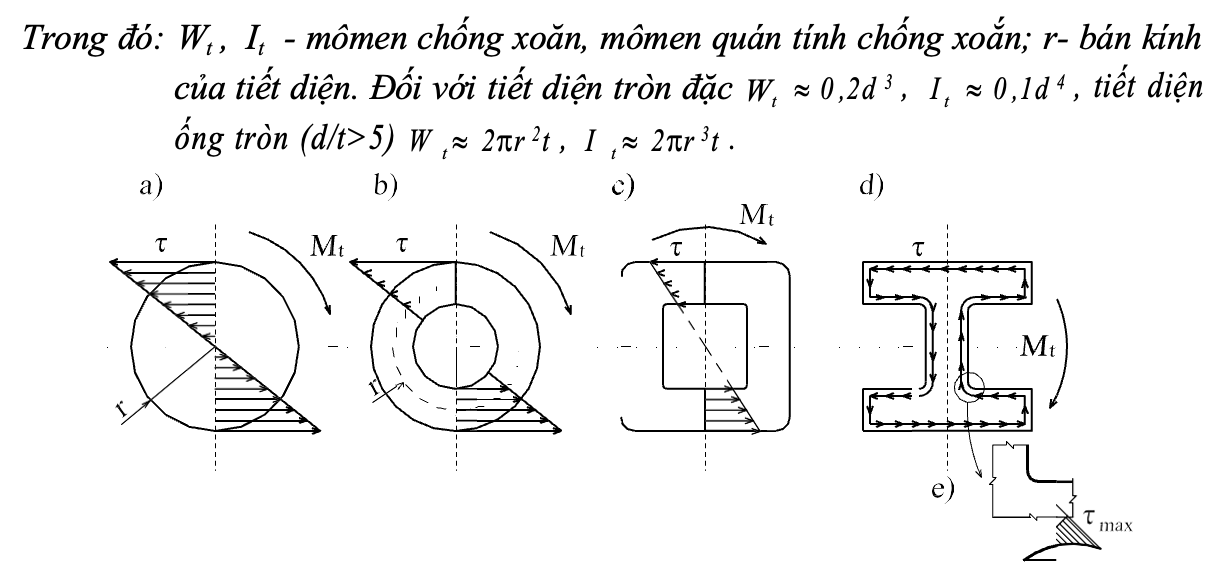
Hình 3.23. Phân bố ứng suất trong tiết diện cấu kiện chịu xoắn: a-tiết diện đặc; b, c – tiết diện kín; d- tiết diện hở; e-tập trung ứng suất tại góc
Khi xoắn một thanh có tiết diện hở bất kỳ, như tiết diện chữ I, C (h nh 3.23,d) It    b t 3 / 3 , với  là hệ số điều chỉnh theo tiết diện: =1,3 đối với thép cán chữ I; =1,5 đối với dầm thép tổ hợp hàn có sườn gia cường; =1,12 đối với thép chữ C, =1,0 đối với thép góc.

Công thức (3.36) chưa xét tới sự tập trung ứng suất tại góc tiết diện (hình 3.23 ,e). Theo nghiên cứu của E.Treffsa [15], ứng suất tại đó có thể tính như sau:

Xoắn tự do (hình 3.24,a) các tiết diện xoay đối với nhau, các điểm của tiết diện chuyển vị không giống nhau theo trục thanh. Tiết diện không còn phẳng nữa và
sẽ vênh, đó là sự vênh của tiết diện ngang. Nếu thanh có điều kiện sao cho mọi tiết diện ngang đều vênh giống nhau, tức là các thớ nằm giữa hai tiết diện ngang không bị biến dạng, thì không có ứng suất pháp; ứng suất tiếp trong mọi tiết diện ngang là giống nhau, còn gọi là sự xoắn thuần túy.

Nếu do điều kiện liên kết gối tựa mà các tiết diện không thể vênh tự do thì các thớ giữa hai tiết diện có những biến dạng dọc khác nhau, sẽ xuất hiện ứng suất pháp và ứng suất tiếp phụ. Đó là sự xoắn kiềm chế hay là xoắn uốn vì có ứng suất pháp của sự uốn.

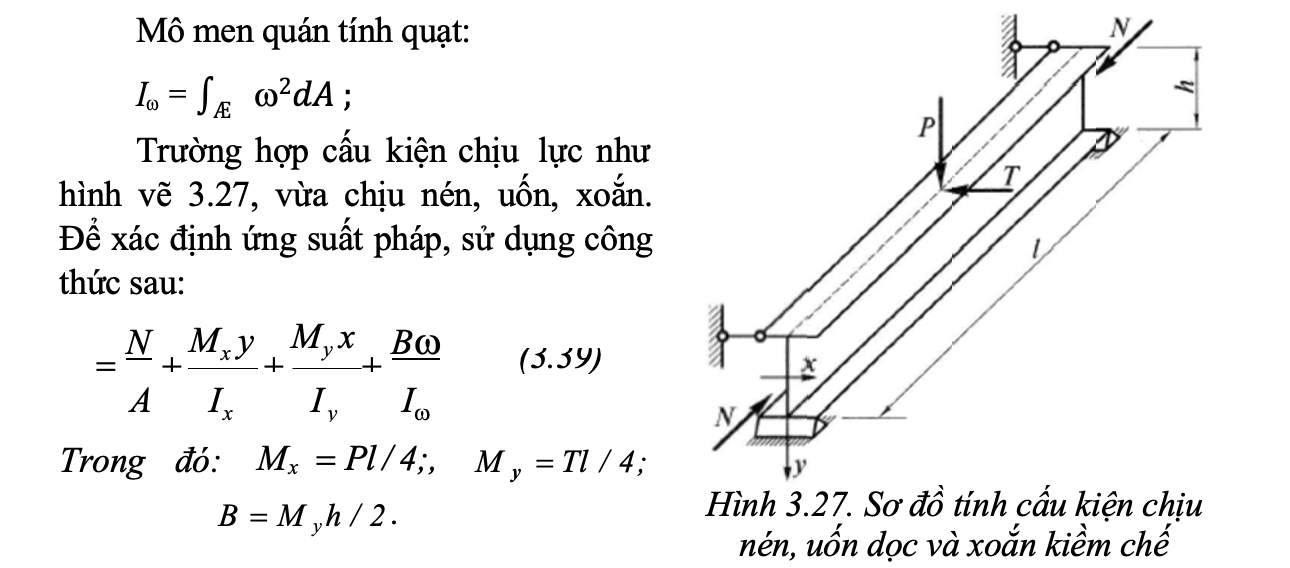
Ví dụ thanh ngàm một đầu (hình 3.24,b): tiết diện ngàm luôn luôn phẳng, càng xa càng vênh nhiều. Biến dạng dọc của các thớ bị hạn chế, làm xuất hiện ứng suất pháp và ứng suất tiếp phụ. Hai cánh bị uốn trong hai mặt phẳng theo 2 chiều khác nhau. Ứng suất pháp trong trường hợp này:

Để nghiên cứu trạng thái ứng suất xoắn uốn, ngoài các đặc trưng của thanh thường, cần một số đặc trưng hình học của tiết diện thanh mỏng hở, xem xét ở dưới đây:

Bimômen xuất hiện khi xoắn kiềm chế. Toàn bộ tiết diện quay quanh trục dọc, mỗi cánh dầm uốn trong mặt phẳng của chúng. Trong mỗi cánh có ứng suất uốn, tạo nên 2 ngẫu lực trong các mặt phẳng cánh, song song và cách nhau là h (chiều cao tiết diện) (hình 3.25).

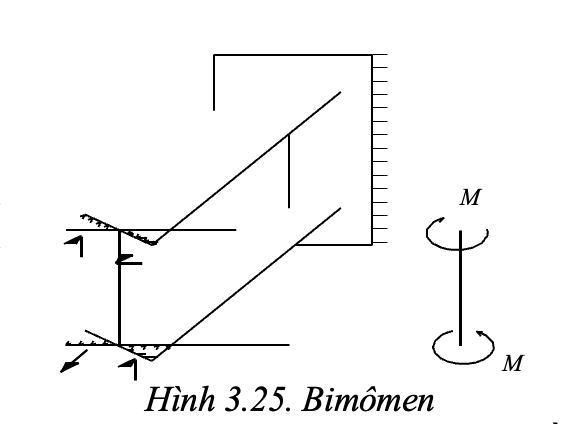
Tích của M này với khoảng cách giữa chúng gọi là Bimômen B, là một hệ gồm 4 lực (2 cặp ngẫu lực) tự cân bằng nhau nên trong các phương trình cân bằng không xuất hiện và không xác định được, muốn tìm nó phải xác định qua biểu thức của góc xoắn (z) là hàm của tọa độ z.

Khái niệm tọa độ quạt. Xét tiết diện hở, tâm O. Ox và Oy là trục quán tính chính trung tâm.
Trên hình 3.26, chọn một điểm A gọi là cực. Một bán kính vectơ tùy ý AM0 làm bán kính ban đầu. Điểm M(x,y) bất kỳ trên đường trung bình của tiết diện, bán kính AM là bán kính chạy. Hai lần diện tích quạt AMM0 gọi là tọa độ quạt  của điểm M.
Quy ước dấu  là dương nếu quét từ AM0 đến bán kính chạy theo chiều kim đồng hồ. Vậy một điểm M là có 3 tọa độ x, y và . Lấy bán kính AM0 ngắn nhất gọi là bán kính ban đầu chính; điểm M0 gọi là điểm quạt chính. Lại chọn điểm A sao cho Ix và Iy bằng 0, A gọi là cực quạt.